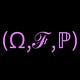On Generative Adversarial Networks (GANs)
In this post, we talk about Generative Adversarial Networks (GANs) which are a pair of neural networks designed to compete with each other in a game theoretic manner so as to achieve an equilibrium.
1. Introduction:
- Generative Adversarial Networks (GANs) are a class of machine learning models that consist of two neural networks, the Generator and the Discriminator, which are trained in a competitive manner.
- GANs were introduced by Ian Goodfellow and his colleagues in 2014 and have since revolutionized the field of generative modeling and artificial intelligence.
2. Basic Concept:
- The key idea behind GANs is to have two networks, one that generates data (the generator) and another that evaluates the authenticity of the generated data (the discriminator).
- These networks are trained together in a game-like setup where the generator tries to create data that is indistinguishable from real data, and the discriminator tries to correctly classify real data from generated data.
Generator:
- The generator takes random noise as input and produces synthetic data that ideally resembles real data.
- The generator's goal is to learn the underlying data distribution so that its generated samples are convincing and can't be easily separated from real data.
Discriminator:
- The discriminator (adversary) receives both real and generated data as input.
- It attempts to classify real data from fake data.
- It's goal is to become adept at distinguishing generated data, forcing the generator to improve its output quality.
3. Mathematical Formulation:
- Objective of GANs:
Given a dataset X with the true data distribution 𝓅(x;data), GANs aim to learn a generator 𝒢 that produces data samples 𝒢(x;ε) from a random noise ε~𝓅ₑ such that the distribution of 𝒢(x;ε) approximates 𝓅(x;data).
- Mathematically,
A generator 𝒢:ℰ→X is a differentiable map from the noise space (ℰ) to the data space (X).
A discriminator 𝒟:X→[0,1] is another differentiable map that takes data samples x as input and outputs a probability 𝒟(x) that x is a real data sample.
The MINIMAX Game:
- The GAN training involves a minimax game between G and D, where G tries to minimize the discriminator's ability to differentiate real from generated data, and D tries to maximize its ability to classify correctly.
- The objective function for GANs is given by the Jensen-Shannon divergence between the true data distribution and the distribution of generated data:
V(𝒟,𝒢):=𝔼(log𝒟|𝓅(⋅,data))+𝔼(log(1−𝒟(𝒢(ε)))|𝓅ₑ).
- The Optimal Solution is:
min max V(𝒟,𝒢) where min is over 𝒢 and max is over 𝒟.
- At equilibrium, the generator produces data that is indistinguishable from real data.
4. Training Algorithm:
- Initialize 𝒢 and 𝒟 with random weights.
- Alternate between the following steps until convergence:
a. Update 𝒟 to maximize V(𝒟,𝒢).
b. Update 𝒢 to minimize V(𝒟,𝒢).
Some notes on GANs:
- The GAN training process involves iteratively improving the generator to produce realistic data while simultaneously improving the discriminator's ability to distinguish real from generated data.
- Training GANs can be challenging and may require careful tuning of hyperparameters and regularization techniques to achieve stable and high-quality results.
5. An application:
One popular real-life application of Generative Adversarial Networks (GANs) is image generation. Let's consider an example of generating realistic human faces using GANs.
Objective: Generate realistic human faces that resemble real images.
Code Snippet:
If you are still here (or even not), thank you for reading! See you in my next post!